In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline.
The slope is defined as the ratio of the "rise" divided by the "run" between two points on a line, or in other words, the ratio of the altitude change to the horizontal distance between any two points on the line. Given two points (x1,y1) and (x2,y2) on a line, the slope m of the line is(slope formula)
Through differential calculus help , one can calculate the slope of the tangent line to a curve at a point.
The concept of slope applies directly to grades or gradients in geography and civil engineering. Through trigonometry, the grade m of a road is related to its angle of incline θ by

- Let's see a example help solving slope of a line problems in algebra ii
One Rental car company charges $35 a day and $0.15 per mile .Rental car company #2 offers $20 an day and $0.35 a mile.Which agency should you choose and what is their slope?.Let y=total cost and x= # of miles.
Answer:-
Company 1 :
Daily Rent = $35
Rent per mile = $0.15
y = 35+0.15x
x: 10 50 100
y: 36.5 42.5 50
gradient = 0.15
Company 2:
Daily Rent = $20
Rent per mile = $0.35
y = 20+0.35x
x: 10 40 100
y: 23.5 34 55
Gradient = 0.35

So ,it we need for longer root(more than 80 miles) the first company is profitable.For shorter root ,the second company is profitable
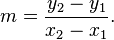




No comments:
Post a Comment